Il était évidemment impossible de réaliser des expériences sur la résonance sur des ponts, afin de répondre à la problématique il nous fallait pouvoir faire le lien entre le phénomène de résonance mécanique théorique et les ponts. Pour cela nous avons contacter la Direction Départemental de l'Equipement qui nous a orientés vers le bureau d'études "EEG SIMECSOL". Ces derniers nous ont fait parvenir des documents issus de la revue Ouvrages d'Art. Ces documents expliquent comment calculer la fréquence propre d'un pont et comment réagit un pont à la marche de piétons, comment atténuer le phénomène de résonance. Dans cette partie nous allons donc essayer de synthétiser et d'expliquer les méthodes de base de calculs :
- Il semblerait que pour calculer les fréquences propres d'un pont, il faille utiliser des logiciels de calcul dynamique, ceci est surtout valable pour les ponts suspendus, les passerelles. Les ponts dits classiques (tablier plus piliers), quant à eux, se contentent de calculs plus simples. Cependant la précision des calculs laisse encore à désirer puisque on ne s'aperçoit souvent qu'après la construction que le pont ou la passerelle rentre aisément en résonance, ce fut le cas pour quelques ponts de la ligne TGV Paris-Lyon et plus récemment la passerelle Tolbiac à Paris qui dut être fermée cinq minutes après son inauguration. Néanmoins lors de grands ouvrages d'art comme le pont de Normandie, on réalise des essais en soufflerie et on utilise les moyens considérables dont dispose l'aéronautique pour modéliser les oscillations du pont.
2. Pour des structures assez simples comme une passerelle on peut utiliser une formule qui est analogue à celle donnant la fréquence propre (relation n°1)du ressort qui est ...

E: module d'élasticité du matériau
I: inertie de flexion de la passerelle
w: masse linéique de la passerelle
l: longueur de la passerelle
lambda: coefficient adimensionnel (explication ci dessous)
...à part qu'elle est multipliée par une constante qui dépend du r-ième mode de résonance de la passerelle, c'est à dire de la r-ième harmonique de la fréquence propre. Cette constante dite "coefficient adimensionnel" est donnée par le tableau ci-dessous la ligne numéro 2 et est susceptible de nous intéresser car elle schématise une passerelle soutenue à chaque extrémité. D'autre part, dans l'hypothèse où l'on aurait pu connaître la raideur de flexion du réglet, en utilisant la première case en haut à droite qui correspond au modèle du réglet en oscillations libres et qui donne la constante lambda, on aurait pu calculer de manière théorique la fréquence propre du réglet.
La raideur de flexion, analogue à la constante de raideur du ressort, est donnée par la formule suivante:
On peut vérifier la validité de la relation 1 en regardant la concordance des unités:
Dans la formule donnant la période propre du ressort
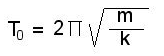
On a m en kg ; et k en N/m or les newtons sont aussi des kg.m/s² car d'après la deuxième loi de Newton on a : ma=F Fen Newton ; a en m/s² et m en kg. T est donc en secondes.
Dans la relation (1) E est en N/m² c'est à dire en kg/m/s², I est en m^4, w est kg/m enfin l à la puissance 4 est donc en m^4. Il nous reste donc des kg.m^3/s² sur des kg.m^3 ce qui donne des s-², après application de la racine carrée il reste donc des /s soient des Hertz (unité de la fréquence).
Après calcul il faut s'assurer que la fréquence propre de la passerelle ne soit vraiment pas comprise entre 1 et 3,6 Hertz, fréquence à laquelle des piétons peuvent mettre en mouvement la passerelle. Pour sortir la passerelle de cette "mauvaise" fréquence il faut jouer sur le module d'élasticité de la passerelle en la rigidifiant. Pour cela si la passerelle est constituée de dalles en béton, on peut les remplacer par une dalle unique cette modification augmente la fréquence, ou encore on peut alourdir le tablier ce qui entraîne une baisse de la fréquence.Pour les ponts suspendus comme le "Pont de Normandie" on leste les câbles afin d'amortir les oscillations (voir exp 2)